|
세계측지계
제3장 좌표변환
3.1 좌표변환모델
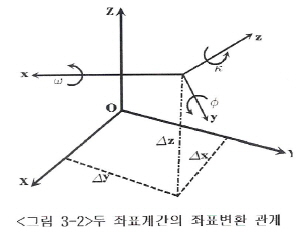
두 좌표계간의 변환은 두 좌표계에서의
위치를 제각기 3차원 직교좌표계(X,Y,Z)로 변환하여 이들간의 차이가
최소가 되도록 변환 파라메터(7매개변수)를 구해야 한다. 좌표변환 모델로서는
Bursa-Wolf, Molodensk-y, Veis 등의 모델이 있다.
(1) Bursa-Wolf 모델
Bursa-Wolf 모델은 두 3차원 직교좌표계간의
좌표계원점에 대한 이동량 및 좌표축 의 회전량을 구하는 방식이다.
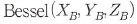 좌표계와 좌표계와
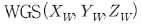 좌표
계간의 원점이 일치하도록 평행 이동시킬 경우의 원점이동량의 3가지
성분 (△X,△Y,△Z)을 두 좌표계간의 좌표축 방향이 일치하도록 X⇒Y⇒Z축의
순서로 변환한다. 회전시킬 경우의 회전량 3성분 좌표
계간의 원점이 일치하도록 평행 이동시킬 경우의 원점이동량의 3가지
성분 (△X,△Y,△Z)을 두 좌표계간의 좌표축 방향이 일치하도록 X⇒Y⇒Z축의
순서로 변환한다. 회전시킬 경우의 회전량 3성분 과
두 좌표계간의 축척변경 △S 등이다. 이와 같이 변환 파라메터를
이용하여 지역좌표계(BESSEL)와 WGS-84좌표계의 변환관계를 행열식으로
표현하면 식 (3.1)과 같다. 과
두 좌표계간의 축척변경 △S 등이다. 이와 같이 변환 파라메터를
이용하여 지역좌표계(BESSEL)와 WGS-84좌표계의 변환관계를 행열식으로
표현하면 식 (3.1)과 같다.
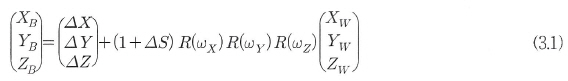
회전행열 R=R(Wx)R(Wy)R(Wz) 의 연산을
수행하고 Wx'Wy’Wz와가 미소량임을 감안하면 결과적으로
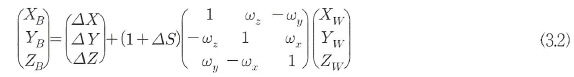
위 식은 동일지점에서 각각의 3차원직교좌표,
즉 Bessel 좌표로부터 구한 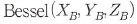 및
GPS관측에 의한 및
GPS관측에 의한 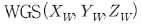 를
기지량으로 하여 7개의 미지변수를 결정한다. 즉 좌표계간 원점이동량
( △X,△Y,△Z) 축척변화율(△S),그리고 좌표축의 회전량 를
기지량으로 하여 7개의 미지변수를 결정한다. 즉 좌표계간 원점이동량
( △X,△Y,△Z) 축척변화율(△S),그리고 좌표축의 회전량 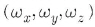 를
결정한다. 따라서 최소 3점(현행좌표 및 WGS-84좌표를 동 시에 알고
있는 점을 의미) 이상에서의 관측치를 확보하면 7개의 미지변수를 결정할
수 있다. 즉, 현행좌표가 알려진 삼각점에서 GPS관측을 하여 WGS-84
좌표를 결정 하였을 경우 이들이 변환파라메터 계산에 활용될 수 있는
점들이다. 이로부터 미지변수, 즉 좌표변환을 특징짓는 7변환변수가
결정되며 GPS관측에 의한 WGS-84좌표가 있는 점에 적용함으로써 이들
점에서의 현행좌표를 계산할 수 있게 된다. 를
결정한다. 따라서 최소 3점(현행좌표 및 WGS-84좌표를 동 시에 알고
있는 점을 의미) 이상에서의 관측치를 확보하면 7개의 미지변수를 결정할
수 있다. 즉, 현행좌표가 알려진 삼각점에서 GPS관측을 하여 WGS-84
좌표를 결정 하였을 경우 이들이 변환파라메터 계산에 활용될 수 있는
점들이다. 이로부터 미지변수, 즉 좌표변환을 특징짓는 7변환변수가
결정되며 GPS관측에 의한 WGS-84좌표가 있는 점에 적용함으로써 이들
점에서의 현행좌표를 계산할 수 있게 된다.
(2) Molodensky 모델
3차원 직교좌표계상의 임의의 한점을
고정시키고 이에 대한 회전량 및 이동량을 구하는 방식이다.
(3) Veis 모델
측량지역 중심의 점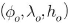 을 중심으로 하는 변환방법으로 좌표성과를 국소지평좌표계에서의 방위각과
경위도의 미소변화량인 연직선편차를 추출할 수 있는 방식이다.
을 중심으로 하는 변환방법으로 좌표성과를 국소지평좌표계에서의 방위각과
경위도의 미소변화량인 연직선편차를 추출할 수 있는 방식이다.
3.2. 모델별 좌표변환방법
좌표변환이란 어떤 좌표계상의 위치를
다른 좌표계상의 위치로 변환하는 작업을 말한다. 좌표계라 함은 지구상의
위치를 수치로 표현하기 위하여 약속한 체계로써,측지좌표계의 경우
경도,위도,표고 또는 타원체면으로부터의 높이로 지구상의 특정 위치를
표기하고 있다. 또한 평면직교좌표의 경우에는 특정의 투영원점에 대한
남북 및 동서 방향의 거리와 표고로 표기하고 있다.GPS에 의하여 결정한
위치는 WGS-84좌표계이므로 우리나라에서 채용하고 있는 Bessel좌표계와
차이가 있으므로 GPS 측량성과를 직접 활용할 수 없다. 즉 동일한 위치일
경우에도 경위도 및 평면직각좌표의 위치와 표시하는 수치가 다르게
나타나므로 측지좌표계 상호간의 변환이 필요하다. 변환방법은 두 타원체간,즉
지역타원체와 WGS-84타원체간의 변환파라메타를 이용하여 지역타원체에
준하여 계산된 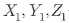 을
WGS-84타원체에 준한 3차원직교좌표 을
WGS-84타원체에 준한 3차원직교좌표 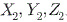 로
변환한다. 변환파라메타로서는 두 타원체간의 원점 이동량(△X,△Y,△Z),
좌표축의 회전량 로
변환한다. 변환파라메타로서는 두 타원체간의 원점 이동량(△X,△Y,△Z),
좌표축의 회전량 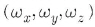 ,
축척계수 등의 7변수를 채용하거나 원점이동량을 고려한 일부만 채용하기도
한다. 그러나 우리나라에서는 특히 지역좌표계로서 채용하고 있는 Bessel
타원체상의 지오이드에 대한 연구가 미흡하여 정확한 변환파라메타의
결정이 어려운 실정에 있다. GPS 위성궤도는 WGS-84타원체[장반경(a):
6378137m,단반경(b): 6356752,편평률(f): 1/298]로 주어지고 있다.
그러나 우리나라의 측지좌표계는 베셀타원체[장반경(a) : 6377397,단반경(b)
: 6356079, 편평률(f) : 1/299]를 사용하고 있다. 따라서 WGS 84좌표계에
의한 지심좌표계로서 현재 우리가 사용하고 있는 뱃셀 타원체에 준거한
경위도 좌표계는 타원체의 중심과 축의 방향이 다르기 때문에 지역에
따라 약 750m정도의 차이가 발생한다. GPS 관측결과를 지적측량 기준점
성과로 실용화하기 위해서는 WGS 84 위성성과를 지적좌표계인 Bessel
타원체를 기준으로한 성과로 좌표 변환하여야 한다. 좌표를 정의하기
위해서는 지구를 수학적인 타원체의 형태로 모델링하여야 한다. 세계
각국에서는 동일한 지구에 대해 서로 다른 타원체 모델을 정의하여 지역측지기준(Local
Geodetic Datum)으로 사용하고 있다. 그러나 현재는 지구전체를 질량중심을
기준으로 하는 세계공통타원체인 WGS-84(World Geodeic System,1984)를
활용하고 있다. 먼저 타원체가 결정되면 종이 지도나 모니터 화면상에
나타내기 위해 평면상에 투영한다. 타원체를 평면상에 투영하는 투영기법으로는
투영면의 형태에 따라 크게 원통도법 원추도법 및 방위도법으로 나눌
수 있다. 우리나라에서 주로 사용되는 투영법은 횡축 메르카토르투영법(Transverse
Mercator Projection),람벨트 등각 원추투영법(Lambert Conformal Conic
Projection)이 있다. 각각의 투영기법에 따른 좌표계로는 국제횡단메르차토르좌표계
(Universal Transverse Mercator Coordinate),평면직각좌표계,세계지리좌표체계(World
Geographic Reference System)등이 있다. GPS에 의한 측위결정은 반드시
우리나라의 측지좌표계의 성과로 변환하며 좌표변환 방법에는 일반적으로
변환요소(7 Parameter)방법, MRE(회귀다항식변환)방법, Molodensky방법
등이 있다. 가장 먼저 GPS 위성에서 관측된 WGS-84좌표계의 ,
축척계수 등의 7변수를 채용하거나 원점이동량을 고려한 일부만 채용하기도
한다. 그러나 우리나라에서는 특히 지역좌표계로서 채용하고 있는 Bessel
타원체상의 지오이드에 대한 연구가 미흡하여 정확한 변환파라메타의
결정이 어려운 실정에 있다. GPS 위성궤도는 WGS-84타원체[장반경(a):
6378137m,단반경(b): 6356752,편평률(f): 1/298]로 주어지고 있다.
그러나 우리나라의 측지좌표계는 베셀타원체[장반경(a) : 6377397,단반경(b)
: 6356079, 편평률(f) : 1/299]를 사용하고 있다. 따라서 WGS 84좌표계에
의한 지심좌표계로서 현재 우리가 사용하고 있는 뱃셀 타원체에 준거한
경위도 좌표계는 타원체의 중심과 축의 방향이 다르기 때문에 지역에
따라 약 750m정도의 차이가 발생한다. GPS 관측결과를 지적측량 기준점
성과로 실용화하기 위해서는 WGS 84 위성성과를 지적좌표계인 Bessel
타원체를 기준으로한 성과로 좌표 변환하여야 한다. 좌표를 정의하기
위해서는 지구를 수학적인 타원체의 형태로 모델링하여야 한다. 세계
각국에서는 동일한 지구에 대해 서로 다른 타원체 모델을 정의하여 지역측지기준(Local
Geodetic Datum)으로 사용하고 있다. 그러나 현재는 지구전체를 질량중심을
기준으로 하는 세계공통타원체인 WGS-84(World Geodeic System,1984)를
활용하고 있다. 먼저 타원체가 결정되면 종이 지도나 모니터 화면상에
나타내기 위해 평면상에 투영한다. 타원체를 평면상에 투영하는 투영기법으로는
투영면의 형태에 따라 크게 원통도법 원추도법 및 방위도법으로 나눌
수 있다. 우리나라에서 주로 사용되는 투영법은 횡축 메르카토르투영법(Transverse
Mercator Projection),람벨트 등각 원추투영법(Lambert Conformal Conic
Projection)이 있다. 각각의 투영기법에 따른 좌표계로는 국제횡단메르차토르좌표계
(Universal Transverse Mercator Coordinate),평면직각좌표계,세계지리좌표체계(World
Geographic Reference System)등이 있다. GPS에 의한 측위결정은 반드시
우리나라의 측지좌표계의 성과로 변환하며 좌표변환 방법에는 일반적으로
변환요소(7 Parameter)방법, MRE(회귀다항식변환)방법, Molodensky방법
등이 있다. 가장 먼저 GPS 위성에서 관측된 WGS-84좌표계의 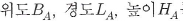 를
WGS-84좌표계의 직각좌표값 (X, Y ,Z)로 변환한 후 WGS-84좌표계의
직교좌표값(X,Y,Z)를 한국좌표계의 직교좌표값 (X,Y,Z)으로 변환한다.
다음은 한국측지계의 직교좌표값(X,Y,Z)를 다시 한국좌 표계의 경도(λ),위도(Ø),높이(H)로
변환한다. 를
WGS-84좌표계의 직각좌표값 (X, Y ,Z)로 변환한 후 WGS-84좌표계의
직교좌표값(X,Y,Z)를 한국좌표계의 직교좌표값 (X,Y,Z)으로 변환한다.
다음은 한국측지계의 직교좌표값(X,Y,Z)를 다시 한국좌 표계의 경도(λ),위도(Ø),높이(H)로
변환한다.
(1) 좌표변환 과정
일반적으로 2개의 측지좌표계간의
변환은 3단계로 나누어서 실시하는 것이 편리하다. 여기서는 “A"측지계로부터
“B" 측지계로 변환하는 방법으로 정리하면 다음과 같다.
① A의 좌표계에 준거한 위도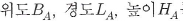 를 직교좌표값(Xa,Ya,Za)으로 변 환한다. 즉 GPS의 세계측지좌표계
WGS-84를 한국측지계(Bess리)로 변환할 경우에는 다음의 과정이 필요하다. GPS로
얻은 위도(B),경도(L),높이(H)를 WGS-84 지심직교좌표값(X1, Y1,Zl)로 계산하면
식(3.3)과 같다. 를 직교좌표값(Xa,Ya,Za)으로 변 환한다. 즉 GPS의 세계측지좌표계
WGS-84를 한국측지계(Bess리)로 변환할 경우에는 다음의 과정이 필요하다. GPS로
얻은 위도(B),경도(L),높이(H)를 WGS-84 지심직교좌표값(X1, Y1,Zl)로 계산하면
식(3.3)과 같다.
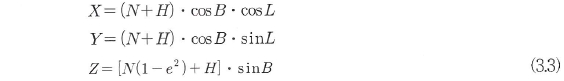
여기서,Xx, Y, Z는 점의 위치를
나타내는 좌표,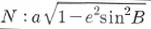 , B: 위도, L: 경도, H: 타원체로부터의 높이 , B: 위도, L: 경도, H: 타원체로부터의 높이

② 다음의 변환공식을 이용해서 b의 직교좌표계로 변화한다.

식(3.4)는 어느 측지좌표계로부터
측지좌표계로 변환하는 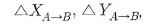 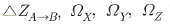 및 S로
7개의 파라매타가 펼요하다는 것을 나타낸다. 우리나라의 측지계인 경우에는 식(1.82)은
그대로 사용하지 않고 회전과 축척의 왜곡은 없다고 보고 식(3.6)으로 정리할 수
있다. 및 S로
7개의 파라매타가 펼요하다는 것을 나타낸다. 우리나라의 측지계인 경우에는 식(1.82)은
그대로 사용하지 않고 회전과 축척의 왜곡은 없다고 보고 식(3.6)으로 정리할 수
있다.

③ 마지막으로 (식.7)응 이용해서 "B"측지계의 위도, 경도,
높이를 계산한다.
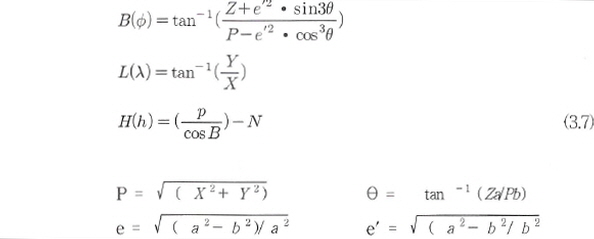
(2) 변환요소방볍 (7 -Parameter)
GPS 측량에 의한 성과를 지적측량
기준점으로 활용하기 위한 성과로 변환해야한다. 최소제곱법에 의하여 산출된
7개의 변환 계수를 7 - Parameter변환방법을 적용하여 상이한 두 직각좌표간의 좌표를
변환한다. 즉,우리나라 측지계(Xkd)와 WGS 84 좌표계 (X84)간의 변환 방정식은
3D-Helmet 변환으로 구성할 수 있다. 변환요소는 선형이동량
(△x,△ν,△z
), 회전이동량(w,¢,k)과 축척계수 S를 이용하여 최소제곱법으로 산출하여 변환한다. 변환방법으로
7 -Parameter를 이용한 기본식은 (3.8) 과같다.

여기서, Xkd :우리나라측지계의
직각좌표계 성분벡터(Xkorea Datum의 약자) X84 :세계측지계의
직각좌표계 성분벡터
△x : 우리나라 측지계와 세계측지계의
원점 편차량에 의한 직각좌표계 성분벡터
S: 두 측지계간의 Seal 차이
ω,¢,k : 각각 X. Y. Z축에서의
회전각을 의미한다.
그리고 [R] 은 두측지계간의 회전을
나타내는 회전행렬(matrix)이다.
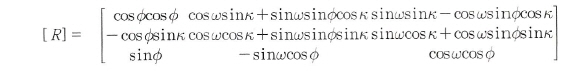
7개의 변환 매개변수와 같은 원리를
이용하여 6개,4개 또는 3개의 매개변수를 이용하는 변환요소를 이용하여 변환을
수행할 수도 있다. Parameter는 기존의 지적기준점을 전국적으로 고른 밀도로 선정하여
GPS관측을 시행한다.
삼각점에 포함된 과대오차를 제거하고
보정하여 높은 정확도의 계수를 확보하고 좌표변환을
위해서는 7개의 Parameter를 먼저 결정하여야 한다.
따라서 7개 변환 매개변수인 △X,[R],S를 알면 WGS 84 좌표를 Bessel
좌표로
변환할 수 있다.
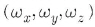 의 3개의 파라미터는
2개의 측지계간의 축방향의 왜곡을 나타낸 것이다. 타원체를 지구에 고정할 때
천체관측이나 방향관측의 오차 또는 기준으로 하는 자오변의 정의로 약간의 왜곡등에
의해 일반적으로 2개의 측지좌표계 축은 평행하지 않다. 2개의 측지좌표계간의
변환을 생각할 경우 지구에 고정된 2개의 회전타원체간의 관계만을 고려하여서는
충분치 않다. 보통 측지계는 타원체를 지구에 고정하고 그 위에 전개된 측지망으로
구성되어 있다. 2개의 측지망간에는 일반적으로 기준이 되는 길이의 차로 인해
계통적인 축척의 비틀림이 생길 경우가 있다. 의 3개의 파라미터는
2개의 측지계간의 축방향의 왜곡을 나타낸 것이다. 타원체를 지구에 고정할 때
천체관측이나 방향관측의 오차 또는 기준으로 하는 자오변의 정의로 약간의 왜곡등에
의해 일반적으로 2개의 측지좌표계 축은 평행하지 않다. 2개의 측지좌표계간의
변환을 생각할 경우 지구에 고정된 2개의 회전타원체간의 관계만을 고려하여서는
충분치 않다. 보통 측지계는 타원체를 지구에 고정하고 그 위에 전개된 측지망으로
구성되어 있다. 2개의 측지망간에는 일반적으로 기준이 되는 길이의 차로 인해
계통적인 축척의 비틀림이 생길 경우가 있다.
이와 같은 경우 축척의 왜곡을 고려하기
위해 S라는 파라미터를 포함한다. 일반적으로 2개의 좌표계원점은 툴리기
때문에 그만몸의 변환을 행하기 위해 △X A→8, △ YA→-8,
△ZA→B의 3개의 평행이동
파라미터가 필요하다.7개의 미지변수,즉 좌표계간 원점이동량 △X,△Y,△Z, 축척보정△S, 그리고 좌표축의 회전량 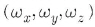 를 구하는 문제는 최소 3점이상에서의
(Xb, Yb, Zb) 및 (Xw' Yw',Zw)를 기지량으로 최소제곱법(least squares method)에
의한 통계처리로써 결정한다. 최소제곱법에 의한 통계처리는 계산에 이용하는
기준점 분포 및 갯수,기준점 성과의 정확도에 따라 변환파라매타가 달리 산출된다는
특징이 있다. 즉,변환파라메터의 산출에 이용할 현행좌표계상에서 정확한 기준점의
선정여부가 변환결과의 정확도에 중요하게 작용하며 좌표변환 계산순서는 다음과
같다. 를 구하는 문제는 최소 3점이상에서의
(Xb, Yb, Zb) 및 (Xw' Yw',Zw)를 기지량으로 최소제곱법(least squares method)에
의한 통계처리로써 결정한다. 최소제곱법에 의한 통계처리는 계산에 이용하는
기준점 분포 및 갯수,기준점 성과의 정확도에 따라 변환파라매타가 달리 산출된다는
특징이 있다. 즉,변환파라메터의 산출에 이용할 현행좌표계상에서 정확한 기준점의
선정여부가 변환결과의 정확도에 중요하게 작용하며 좌표변환 계산순서는 다음과
같다.
① 기지점 좌표 및 미지점 좌표를
입력한다. 이 경우 미리 작성되어 있는 입력데이터 파일을 활용할 수 있다.
② 변환계산을 실행시킨 후 변환파라메터의
크기,오차를 확인하고 기지점에서의 현행성과와 변환성과간의 차이를
조사한다. 이것은 출력파일을 보면 곧바로 알 수 있다.
③ 현행성과와 변환성과간의 차이가
커 기지점 성과가 불량하다고 판정되는 점을 추출한다. 즉,변환파라메터의 계산에서
제외시키기 위해 편집작업을 수행한다.
④ 다시계산 할 경우에는 결과를 검토하여
평방제곱근오차 기지점의 잔차 등을 검토하여 정확하게 변환되었을 경우
계산을 종료한다.
⑤ 미지점의 경우에는 GPS관측에 의한
WGS-84 좌표만 입력되었으므로 변환성과와 현행성과간의 차이를 출력하지
않는다.
⑥ 변환에 제외시켰던 기지점의 경우는
변환성과와 현행성과간의 차이를 출력하여 참고한다.
(3) 회궈다항식 변환기법
본 기법은 두 기준계상의 위성 관측점에
대한 WGS-84 및 우리나라 TM좌표의 직교좌표 성분의△x ,△ν ,△z)를 구하여 이를 독립변수로 하는 4차원 경향별
해석을 통해 보정량을 산출하여 변환을
수행한다. MRE방법은 Tokyo Datum(우리나라 포함)을 WGS 84로 변환하는
식이며 좌표보정 량을 구하여 Tokyo Datum에 기준한 좌표값에 더해 주면 WGS 84좌표계를
얻을 수 있다. WGS-84 좌표에 보정량를 더해줌으로서 우리나라 적각좌표를
얻는다.
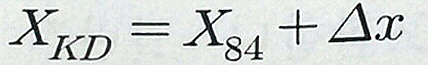

(4) Molodensky법
두기준계상의 위성 관측점에 대한
WGS-84 및 Bessel 타원체에 준거한 경위도좌표의 편차량 (△ λ˝, △Ф˝,
△H")을 Molodensky 변환식으로 도출하고 이를 보정하여 두 측지계간의 변환을 수행한다.

3.3. 우라 나라 좌표변환 방법
현재 우리나라는 기존의 기준점이나
수치지형도의 좌표변환방법에서 발생되는 문제점을 해결하기 위하여 변환계수만을
이용한 좌표변환방법에 왜곡량 모델링 (distortion modelling)을 추가하여
좌표변환시에 발생하는 오차의 문제들을 해결하는 방법이다. 변환방법의 주요 단계와
내용은 다음과 같다.
(1) 세계측지계로의 변환계수(7-변환계수)
결정
상사성(등각성)에 의거한 좌표변환
변환계수를 결정하기 위하여 사용되는 수학적인 모델식들은 Burs a- Wolf, Molodensky-Badekas,
Veis 등 여러 모델식을 사용할 수 있다. 이들 수학적인 모델식들은
미지변환계수를 최소제곱조건에 의하여 계산함으로써 변환계수를 결정한다. 이
단계에서는 상사성에 의거한 좌표변환 변환계수를 결정하기 위하여 구 측지기준(지역적인
측지좌표계)과 새로운 측지기준(세계좌표계) 에 기준한 좌표를 가진 공통점(기준점)을
사용하여야 한다.
전국적으로 일관된 성과를 산출하기
위하여 『국토지리정보원 고시 제2003-497 호』 에 의한 국가변환계수를 준용할
것을 권장한다. 고시된 국가변환 계수는 Molodensky- Badekas 모텔에 의하여
결정된 것이며 그 값은 다음과 같다.
|
구분
|
평행이동량(m)
|
회전량(")
|
축척변화량(ppm)
|
| △x
|
△y
|
△z
|
Rx
|
Ry
|
Rz
|
λ
|
|
변환계수
|
-145.907
|
505.034
|
685.756
|
-1.162
|
2.347
|
1.592
|
6.342
|
그러나 이러한 국가 파라미터는 지역마다
왜곡량의 편차가 달라 일부 지역에서는 검사점의 지도 좌표와 실제 측량 좌표 사이의
차이로부터 RMSE(Root Mean Square Error)를 구하여 평가를 하게 되면
규정보다 큰 오차가 발생할 수 있으므로 이러한 오차 발생시에는 지역파라미터를
사용하여 좌표변환을 실시해야 한다.
(2) 수치지형도의 평면직각좌표를
측지좌표로 변환
좌표변환을 실시하고자 하는 평면직각좌표(TM투영의
Gauss- Kruger 투영식)를 다양한 데이터 파일포멧(DXF, NGI)을
읽어 역투영식에 의하여 측지좌표(또는 지리좌표)로 계산한다. 수치지적도는
CAD나 GIS소프트웨어에서 제공되는 다양한 포멧을 사용하여 제작되었거나 편집되었으므로
수치지적도상의 객체들의 위치좌표는 평면직각좌표로 표시되어 있다. 따라서
각 객체들의 평면직각좌표를 역 TM투영식에 의하여 측지좌표(지리좌표 또는 경
· 위도 좌표)로 계산하고 계산된 측지좌표는 3차원 직각좌표계에 기준한 3차원 직각좌표로
변환한다.
측지좌표를 3차원직각좌표로 변환하는
식은 다음의 식을 사용하도록 한다다
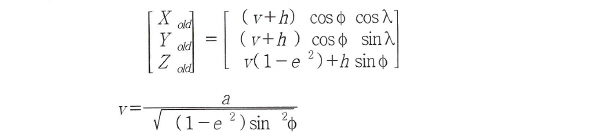
여기서, Ø, λ는 측지좌표(위도,경도)이고,h는 타원체고,e는 편평률,a는 Bessel 타원체의 장반경(6377397.155 m)이다.
(3) 지역측지계에서 세계측지계로의
변환
(2)에서 계산된 3차원직각좌표를
(1)에서 제시한 7개 변환계수를 사용하여 새로운 측지기준인 세계측지계에 기준한
3차원직각좌표로 계산한다. 본 단계에서의 계산식 은 『국토지리정보원 고시 제2003-497호』
에서 제시한 다음의 식을 사용한다.

|
구분
|
기준좌표
|
비고
|
|
Bessel
=> GRS80
|
GRS80
=> Bessel
|
|
X
Y
Z
|
-3.159,521.31
4,068,151.32
3,748,113.85
|
-3,159,666.86
4,068,655.70
3,748,799.65
|
|
(4) 세계측지계에 기준한 3차원 직각좌표를
측지좌표로 역변환
(3)에서 변환된 3차원 직각좌표(
X g, Yg, Zg)를 측지좌표로 역계산한다. 역 계산은 다음의 식을 사용하여 외삽법에 의하여
요구하는 정밀도(10 -6)에 수렴할 때까지 계산하여야 한다.
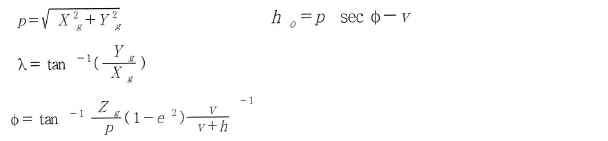
(5) 측지좌표를 평면좌표로 변환
(4)에서 계산된 결과인 측지좌표는
새로운 측지기준인 GRS80타원체에 기준하여 TM투영 법(Gauss- Kruger투영식)으로써
평 면직각좌표를 계산한다.
(6) 왜곡량의 계산
확보된 공통점들에 대하여 (1)에서
(5)의 좌표변환과정을 거쳐 계산된 평면직각좌표와 GPS관측을 통하여 세계측지계에
기준하여 결정된 평면직각좌표간의 차이를 x 축,y축 성분으로 구분하여 계산하고,
이 차이를 X축,y축 “왜곡량”이라고 정의한다. 새로이 채택된 세계측지계에 기준한
수치지형도의 표고기준은 기존의 국가수준기준 면(인천만의 평균해수면)을 준수하므로
표고방향의 왜곡량은 계산할 필요가 없다.
(7) 잔여 왜곡량의 계산과 왜곡량
모델링
(6)에서 결정한 X축,y축 왜곡량의
경향(trend)을 분석하여 선형 및 비선형 회귀식을 사용하여 최소제곱법에 의한 회귀방정식을
결정하고 결정된 회귀방정식 (여기서는 경향방정식이라고 한다)을 사용하여
왜곡량으로부터 경향값을 빼내어 X축,y축의 잔여 왜곡량을 계산한다.
계산된 X축,y축의 잔여 왜곡량을
사용하여 왜곡모델링을 수행하도록 하며, 모델링을 위한 수학적인 함수로서는
최소제곱 콜로케이션법(Least Square Collocation)법을 사용하도록 한다.
최소제곱 콜로케이션법에 의한 왜곡량의 추정을 위하여 각 축의 잔여왜곡량값을 사용하여
경험적인 공분산을 구하고,이들 경험적 공분산값에는 해석적 공분산 함수인
Gaussian 및 Reilly함수를 사용하여 함수의 파라미터들을 결정한 후에 이들을 사용하여
일정한 규격의 격자파일로 각 축의 왜곡량을 모델링한다. 추정한 왜곡량
모델령 결과를 경향방정식에 더한 후에 7개 변환 파라미터에 의하여 변환된 수치지도의
좌표에 보정을 실시한다.
왜곡량 모델링을 포함한 수치지형도의
변환에 관한 일반적인 과정은 그림에 표시한 바와 같고, 왜곡량 모델링에
대한 전체적인 세부단계는 다음과 같다.
■ 수치지형도 제작에 사용된 기준점(국가기준점,항측기준점)의 두 측지기준계간(동경측지계,세계측지계)의 성과를
확보한다. 두 측지기준계간의 성과의 확보가 불가능할 경우에는 기준점 GPS 관측데이터를
두 측지기준계에 따라 재처리한 후에 성과를 확보한다. 만일 GPS 관측데이터가
없는 경우에는 점의 조서상의 기준점 위치에 현장 GPS 관측을 실시하여 위의
방법에 의하여 새로이 성과를 재 계산하여야 한다.
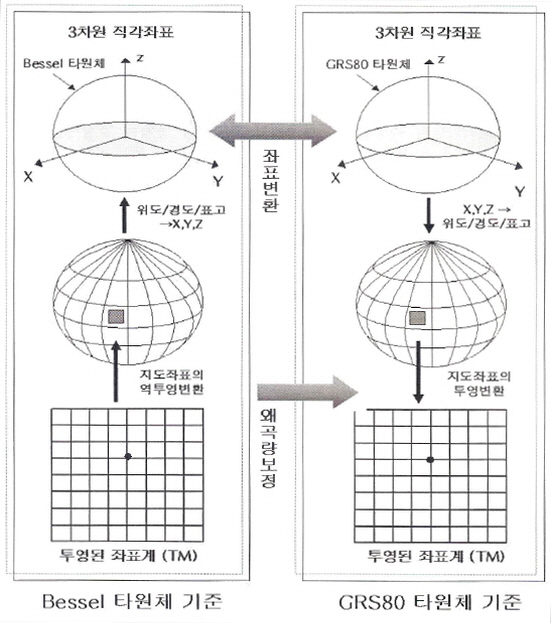
<그림
3-3> 수치지형도의 좌표변환 단계
■ 각 공통점의 성과 중에서 구측지계에
기준한 성과를 (1)의 7개 변환계수와 (3) 에서 제시한 변환식을 사용하여 세계측지계의
성과로 변환을 실시한다. 이 변환성과와 확보한 세계측지계의 성과와의
평면직각좌표계상의 차이를 구하여 x축,y축의 왜곡량을 계산하고 분석
한다.
■ 데이터 품질을 확보하고 일관성을
유지하기 위하여 상사성이 없는점들을 분류 하여 제거한다. 즉,과도하게 왜곡량이
큰 점들은 모델링에서 큰 오차를 발생시 키므로 제거하여야 하는데 그 크기는
2m 정도를 한계값으로 하도록 한다.
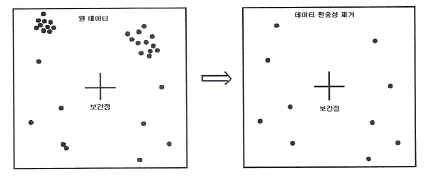
■ 일정한 공간적 분포를 얻기 위하여
데이터의 편중성을 분석하고 편중된 데이터를 제거한다. 이 과정에서 데이터의
편중성을 제거하는 이유는 고르게 분포되지 않은 데이터내의 특정점에서 예측치가
편기되는 문제를 발생시킬 수 있어 불규칙한 데이터 분포로 인한 볼완전한
왜곡 모델링이 수행될 수 있기 때문이다.
■ 편중성이 제거된 데이터의 X축,y축
왜곡량의 경향(trend)을 분석하여 선형 및 비선형 회귀식을 사용하여 최소제곱법에
의한 경향방정식을 결정하고,결정된 방정식을 사용하여 경향값을 빼어
X축,y축의 잔여 왜곡량을 계산한다 .
■ x축,y축의 잔여 왜곡량에 대한 경험적
공분산 함수를 계산한다. 경험적 공분산 함수는 개발된 컴퓨터 프로그램을
사용하며,이 경험적 공분산 함수에 최소제 곱 곡선접합법(Least Square Curve
Fitting)을 적용하여 경험적 공분산 함수들에 대한 해석적 모델을 선택하고,함수의 파라미터인 초기 공분산(분산)값과 특성
거리 (Characteristic Length)를
계산한다. 본 작업 지침에서 사용할 수 있는 해석적 공분산함수식은 Gaussian
공분산 함수 및 Reilly 함수식을 사용하도록한다.
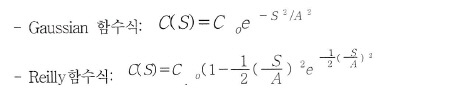
위의 공분산
함수식에서 S는 거리, A는 특성거리, C(o): S=0 일 때에 C(S)로써 취한
값인 초기 분산값이다.
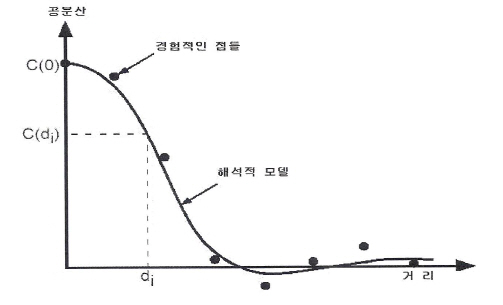
〈그림 3-4> 공분산 함수식에
의하여 표시되는 거리에 따른 공분산 함수의 일반적인 형태
그림<3-4>는 경험적 공분산에
최소제곱법을 적용하여 결정한 해석적 공분산 함수의 최적화와 변환계수인 초기 공분산값(Co)와
특성 거리(A)를 결정하는 것을 표시한 것이다.
(8) 왜곡량의 모델링
결정하고자 하는 왜곡량 모델의 격자파일의
각 격자점에서 x,y 왜곡량 성분을 최소제곱콜로케이션법 및 보간법들을
사용하여 계산한다. 본 지침에서는 최소제곱콜로케이션법에 의한 왜곡량 모델링을
아래식을 사용하여 수행할 것을 권장한다.
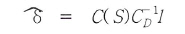
위식에서 켠는 왜곡량이고
벡터 C(S)의 요소들은 데이터 점들과 보간점 간의 거리를 사용하여 위에서 제시한
해석적 공분산 함수로부터 구한다. 또한, 매트릭스 Cd의 요소들은 데이터 점들의
모든 조합에 의한 거리를 사용하여 해석적 공분산 함수로부터 계산된다. 벡터
1은 각 데이터점들에서 왜곡을 포함하고 있는 관측치이다.
위 식을 사용하여 일정한 격자 간격으로
X축,Y축의 잔여 왜곡량의 추정값을 결정하고, 앞에서 결정한 X축,Y축의
경향방정식에 추정된 X축,Y축 잔여 왜곡량을 더하여 최종적으로 왜곡량 모델링을
완료하고,각 축별 왜곡량의 격자파일을 생성 한다.
(9) 좌표의 변환
좌표변환 프로그램은 국토지리정보원에서
제공하는 GDKtrans Ver.2, 국토해양부에서 제작한 세계좌표계변환 프로그램,
지적연수원에서 제작한 좌표변환프로그램 등 여러 가지가 있으며 변환된 결과
값은 많은 차이가 없다. 따라서 여기에서는 국토해양부에서 제작 배포함 세계좌표계변환
프로그램을 사용하여 좌표변환을 실시하기로 한다.
(10) 변환된 수치지형도의 정확도
평가
변환된 수치지형도의 변환 위치 정확도를
평가하기 위해서는 변환된 수치지형도상에서 명확하게 확인이 되는 위치(도로
구획선 등)를 선정하여 현장에서 GPS 측량을 실시하고 비교 · 분석을
실시하여 평가하여야 한다. GPS 측량은 statics 측량을 실시하도록 하며 한 도엽당 최소
1점 이상 검사점을 선정하여 측량을 실시한다.
소정의 정확도를 확보하기 위하여
GPS 위성 신호 수신 시간은 최소 30분 이상을 하도록 한다. GPS 데이터 처리는
세계측지계에 기준하여 성과를 계산한 후 이 계산된 평면직각좌표와 변환 후 생성된
수치지형도상의 평면직각좌표와의 차이를 분석 하여 정 확도를 평가하도록 한다.
좌표를 사용하는 지도,영상지도,DEM(Digital Elevation Models) 등과 같은 성과물의 정확도는 일반적으로 검사점의
지도 좌표와 실제 측량 좌표 사이의 차이로부터 RMSE(Root Mean Square Error)를
구하여 평가를 하게 된다. RMSE를 구하기 위한 계산식은 다음을
따르도록 한다.



|