세계측지계

제2장 측량의 기준

2.1. 측량의 기준면

지구의 형태에는 실제지형과 지오이드 및 타원체의 3가지가 있다. 측지학에서는 지오이드를 지구의 형상으로 채용하는데 이 지오이드는 요철이 있어 삼각측량 등 에 직접 사용할 수 없으므로 측량에서는 지오이드에 거의 유사한 회전타원체를 사용한다.

2.1.1. 물리적 표면(Physical Surface)

지구의 표면은 원래 매우 불규칙한 형상을 가지고 있으나 이런 지구의 형상을 이용하여 지구상의 좌표계는 만들 수 없다. 따라서 지구와 가장 유사하면서 수학적으로 사용할 수 있는 지구의 형상을 결정해야만 한다.

2.1.2. 지오이드(Geoid)

지오이드는 평균해수면을 육지까지 연장해 놓은 가상적인 곡면으로 지구의 밀도가 균일하지 않기 때문에 지오이드 표면도 불규칙한 표면을 이룬다.

지오이드는 등포벤셜면으로 위치에너지 0인 면이며，연직선 중력방향에 수직인 면이다. 육지에서는 지오이드가 타원체보다 위에 있으며，바다에서는 지오이드가 타원체보다 아래에 있다.

2.1.3. 회전타원체와 지구타원체

기준점측량에 있어 기준점의 위치를 표시하는 데는 불규칙한 지오이드로서는 부적당하여 어떤 수학적인 표면을 고려하는 것이 필요하다. 따라서 지구의 실제모양과 흡사한 타원을 고려하고 이 타원의 단축을 축으로 하여 회전하는 회전타원체(Ellipsoid of rotation)를 설정 하였다.

이 회전타원체는 각 지역의 측량결과에 어울리는 크기의 것을 고려하여 이를 회전 타원체， 즉 지구타원체(Earth ellipsoid)로서 우리나라에서는 베셀의 타원체를 쓴 다.(그림 2-1참조)

2.1.4. 준거 타원체 (Reference ellipsoid)

경위도원점에 있어서 베셀(Bessel) 원자를 가진 회전타원체를 그 경위도와 원방위를 가지고 지오이드변에 붙인 것으로서 수준원점의 표고 0m의 곳을 지나도록 하여 이것을 준거타원체로 한다.

우리나라 토지조사사업 당시 삼각점의 경위도는 경위도원점(일본 경위도원점인 동경천문대 자오환의 중심)에 기하여 이 준거타원체를 기준으로 한 성과들이다.

2.1.5. 지오이드와 준거타원체와의 관계

지오이드는 수준측량, 준거타원체는 삼각측량망의 투영기준으로 쓰는 것으로서 이들 2개면을 경위도원점에서 <그림 2-2>와 같이 접합시키고 있다. 천문측량은 지오이드，즉 국지적인 지오이드면에 의하여 어떤 점의 경위도를 측정하나 삼각측량 에서는 관측에 의하여 구한 삼각형의 각과 변장을 기준으로 원점에서 출발하여 기하학적인 계산을 타원체상에 전개하여 점차 삼각점의 경위도를 구한다.

이 경우 삼각측량의 출발점으로 되는 원점의 경위도와 진북에서의 방위각은 천문측량에 의하여 정할 수 밖에 없으므로 원점에 있어서의 연직선편차(Defle-ction of vertical)는 정오차로 되고 그 결과 각 삼각점의 경위도에 영향을 준다. 이와 같은 영향을 피하기 위하여 측지학좌표에서 가장 중요한 것은 타원체를 현실의 지구가 가장 잘 적합하도록 설정하는 것이 필요하다. 이상적인 접합은 다음의 2가지 조간이 만족될 때 이루어진다.

    ① 타원체의 법선과 연직선의 일치
    ② 지구축과 타원체 극축의 평행

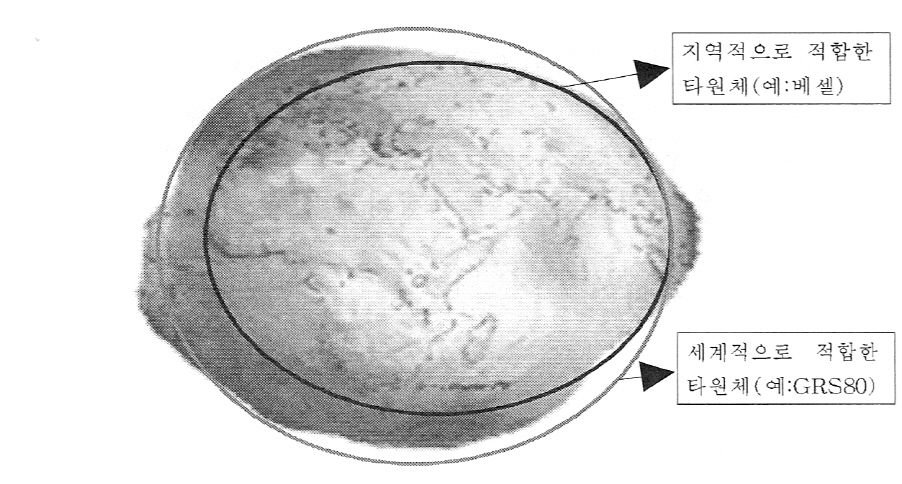
<그림2-1> 지구의 형상

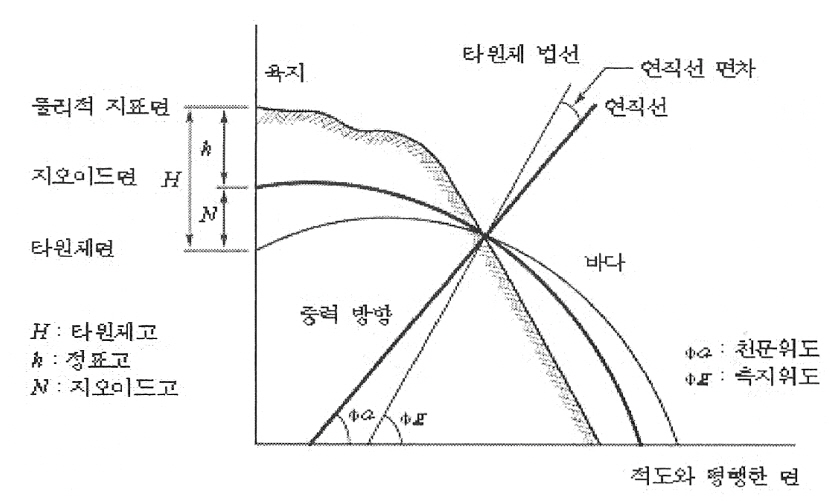
<그림 2-2>지구타원체와 지오이드 관계

2.2. 지구타원체

지구는 극지방이 적도지방보다 약간 편평한 타원체와 유사하며 타원체 중 지구 와 가장 유사한 타원체를 지구타원체라 부른다. 우리나라에서는 1841년 베셀 (Friedrich Wilhelm Bessel)이 발표한 회전타원체값을 지구인자로 사용하여 각종계산에 쓰고 있다. 1924년 마드리드에서 개최된 국제측지학협회(lAG)에서는 지구타원체로서 장반경 a=6.378.388m 편평율 f=1/297.0의 것을 국제타원체로 채용하기로 결정했다. 이것은 미국의 측지학자 헤이포드(J.F .Hayford)씨가 1909년에 정한 것과 같다.

1980년 국제측지학 및 지구물리학연합(IUGG)은 새로이 1980년 측지기준계(1980 geodetic reference system) 재원중 국제지구타원체(International ellipsoid)로서 a=6,378,137m， f=1/298.26을 채용하므로써 지구의 형상과 크기에 대한 기준으로 삼았다. 지구형태의 측정은 여러 사람에 의하여 측정되었다.

2.1.1. 위도와 대원 및 자오선수차

  (1) 위도의 종류

위도는 자오선을 따라 적도에서 어느 지점까지 관속한 최소 각거리로서 어느 지점 의 연직선 또는 타원체의 법선이 적도면과 이루는 각으로서 남북위 0˚~90˚로 표시 한다. 위도에는 천문위도 측지위도 지심위도 화성위도로 구분된다. 경도 1˚에 대한 적도상 거리 즉 위도 0˚인 지점에서의 거리는 약 111km， 1′은 1.85km， 1″는 30.88m이다.

측지위도(測地緯度 : φg)는 지구상 한 점에서 회전타원체의 법선이 적도면과 이루는 각으로 측지분야에서 많이 사용한다. 천문위도(天文違度 : φa)는 지구상 한 점에서 지오이드의 직선(중력방향선)이 적도면과 이루는 각을 말한다.

지심위도(地心違度 : φc)는 지구상 한 점과 지구 중심을 맺는 직션이 도면과 이루 는 각을 말한다. 화성위도(化成違度 : φr)는 지구중심으로부터 장반경( a)을 반경으로 하는 원과 지구상 한 점을 지나는 종선의 연장선과 지구중심을 연결한 직선이 적도면과 이루는 각을 말한다. (그림 2-3 참조)

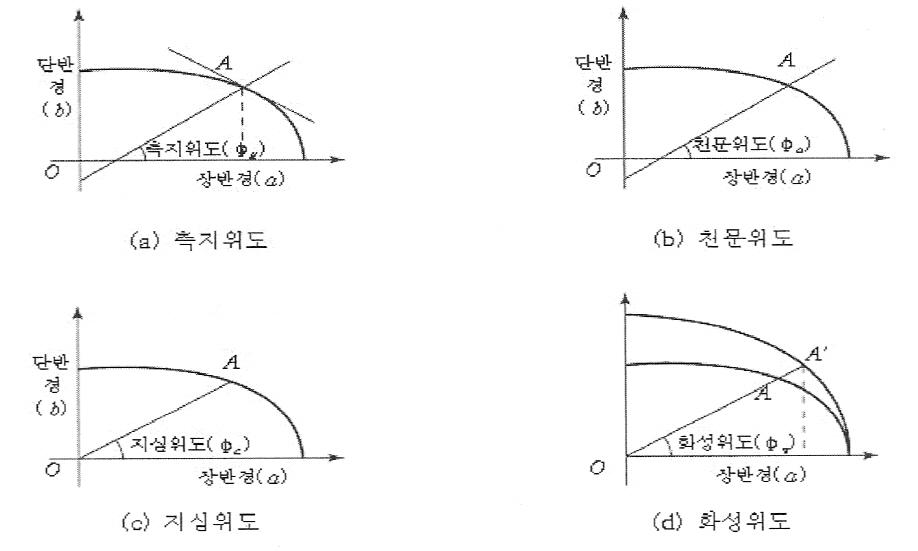
<그림 2-3> 위도의 종류

   (2) 자오선 수차(Meridian Convergency)

  좌표원점에 있어서의 자오선방향(λ)와 어떤 점을 지나는 자오선 방향은 <그림 2-4>에서 보는바와 같이 양극을 맺는 선상에서 교차되어 교각을 갖는다. 이 교각(r)을 자오선수차라 한다.

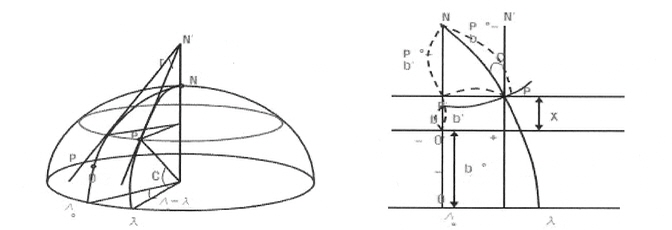
                                       <그림 2-4>                                                                <그림 2-5>

즉 <그림 2-5>에서 N′P는 NO에 평행한 호로 하고 ∠NPN′=C로 하면 구면직각삼삭형 NFP′에서 자오선수차(C)는

       tan C = sin y′ tan b′ ••••••  (2.1)

방위각과 방향각은 원점의 자오선상에 있는 점에서는 일치하나 그 이외의 점에서는 일치하지 않으며 자오선수차 만큼의 차를 발생한다. 그 크기는 그 점이 원점에서 멀리 떨어짐에 따라 증가한다.

어던 점에 있어서 X축에 평행한 방향을 기준하여 표시하는 자오선 방향의 수평각을 진북방향각이라 하며 진북방향각과 자오선수차는 절대치는 같고 부호만 반대이다.

진북방향각은 원점의 동쪽에서는 부(-), 서족에서는 정(+)부호를 갖는다.

<그림 2-6>에서 방위각을 α, 방향각을 T, 진북방향각을 γ로 하면

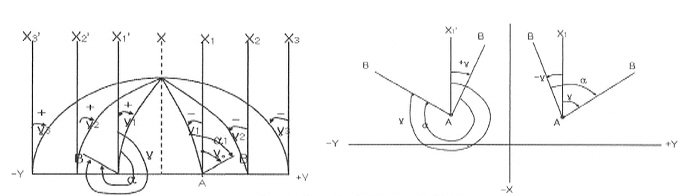
<그림 2-6> 방위각과  방향각

2.3. 한 점의 위치표시법

점의 위치를 표시하는 데에는 지구상의 절대적 지리좌표(Geographic Coordinate)인 경위도로 표시하는 측지좌표방법과 구변직각좌표방식 및 준거타원체상의 점을 평면에 투영하여 평면직각좌표로 표시하는 방법이 있다.

  (1) 경위도좌표

복잡한 기복과 기형을 갖고 있는 지표면상의 모든 점의 위치는 이들의 각 점에서 내린 수선(법선)과 기준타원체의 적도면과 만드는 각인 위도(B;Latitude)와 그 점을 지나는 자오선과 그리니치천문대의 자오환의 중심을 지나는 자오선과 만드는 각 즉 2자오면의 협각인 경도(L; Longitude)로 표시된다. (그림 2-7참고)

위도는 적도변을 0˚로 기준하여 남북 각각 90˚ 씩 잡고 있으며 경도는 기준자오선 (Greenwich meridian)을 O˚로 기준하여 동서로 각각 180 씩 잡고 있다.

경도는 동일 자오선상의 점에 대하여는 모두 같으며 점의 횡(동서)방향의 위치를 정한다.

동일 위도 평행권상에 있는 점의 위도는 모두 같으며 위도를 지정하면 점의 종(남북)방향의 위치가 정해진다.

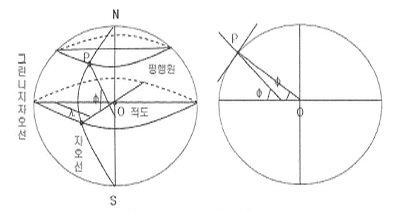
<그림 2-7> 경위도 좌표>

  (2) 구면직각좌표

구면직각좌표(Spherical orthogonal coordinates)는 점의 위치를 구면상에서 직각좌표로 표시하는 방법이다.

구면직각좌표(Spherical rectangular coordinate system)에서는 <그림 2-8>에서와 같이 지구를 구로 보고 좌표원점 O를 지나는 자오선(주자오선) NOS를 X축에 직교하는 대원을 Y축으로 하여 점의 위치를 표시한다.

즉 1점 A의 위치는 A를 지나는 대원이 원자오선(NOS)과 만나는 교점을 A'라할때 자오선 호장  OA'를 X좌표， 대원의 호장 AA'를 Y좌표로 표시한다.

구면상 점의 위치를 나타내는 이 X와 Y는 각도 또는 길이로 표시된다.

X는 원점으로 부터 북에 있는 것을 정(+ )， 남에 있는 것은 부(-)로 하고 Y는 원점의 동쪽에 있는 것을 정(+ )， 서쪽에 있는 것을 부(-)로 한다.

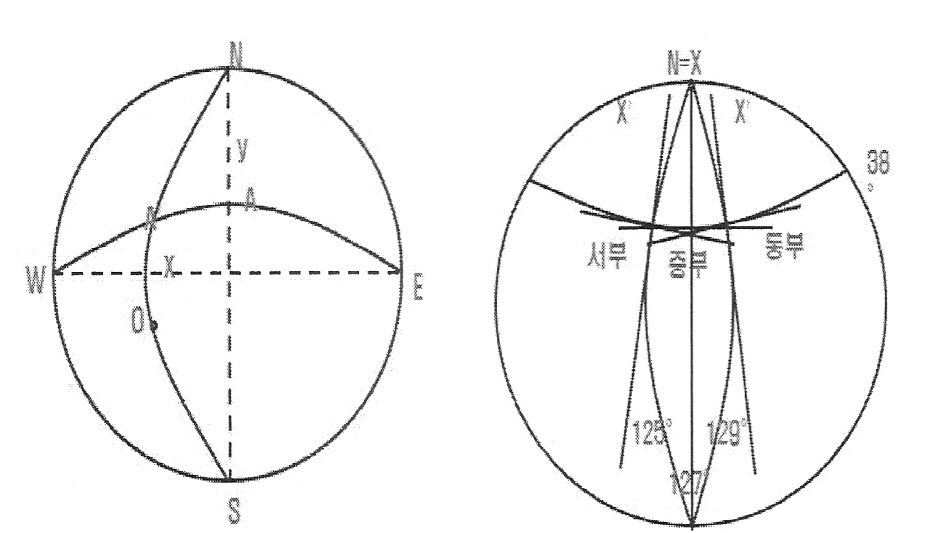
<그림 2-8> 구면직각좌표                           <그림 2-9> 평면직각좌표>

(3) 평면직각좌표

대축척측량에서는 경위도를 그대로 사용하는 예는 거의 없고 이것에 의하여 계산된 평면직각좌표 X,Y에 의하는 경우가 대부분이다.

평면직각좌표계 (plane rectangular coordinate system) 에서는 측량지역에 대하여 적당한 1점을 좌표원점으로 정하고 이점을 지나는 자오선방향(진북방향)을 X축(북,+)，이것에 직각의 방향을 Y축(동,+)으로 하여 가우스상사2중투영법으로 점의 위치를 적각좌표 X,Y로 표시한다.

<그림 2-9>는 우리나라 3대원점에서의 평면직각좌표체계를 중부원점을 기준으로 나타낸 것으로 각 원점자오선은 투영원점(38˚)에서 북쪽으로 올라 갈수록 지구의 북극쪽으로 수렴한다. 따라서 38˚ 이북 지역으로 올라 갈수록(위도가 높을수록) 각 원점별 자오선 사이는 좁아지고(즉 원점사이의 Y값이 적어지고). 38˚ 이남 지역으로 내려 갈수록 각 원점별 X축 사이는 넓어진다(즉 원점사이의 Y값이 커진다)

평면직각좌표의 투영원점의 좌표는 X=0.00m Y=0.00m로 사용하는데，이는 원점의 좌표값을 0m로 (-)의 좌표값이 생겨 계산상 불편함으로 모든 좌표를 X좌표에 500,000(단， 제주도는 550,000m)， Y좌표에 200,000m를 더하는 값을 좌표정수 (coordinate constants)라 한다. 좌표정수는 원점의 값을 500,000m로 하여 계산하는 것이 아니며 원점의 값은 0m로 계산하고 얻어진 결과에 일정한 좌표정수값을 더한다는 것을 유의해야 한다.