Ⅱ.측량수학

1.삼각함수

   1)각도의 단위

    2)삼각함수의 정의

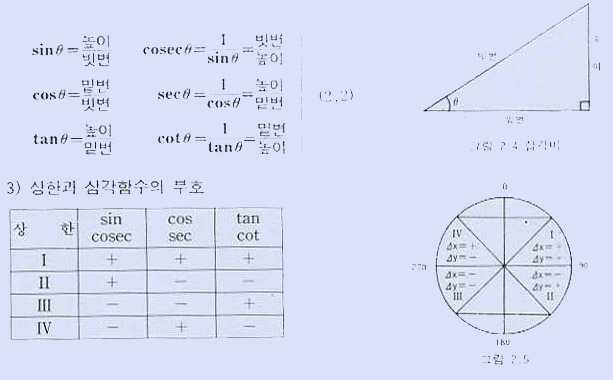
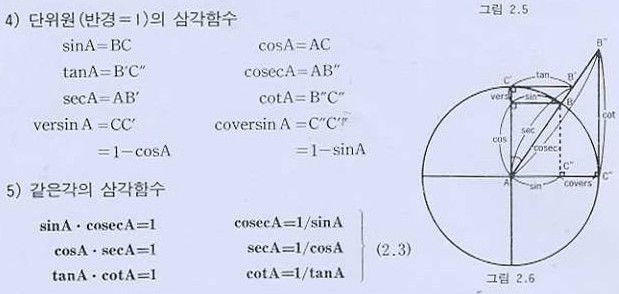
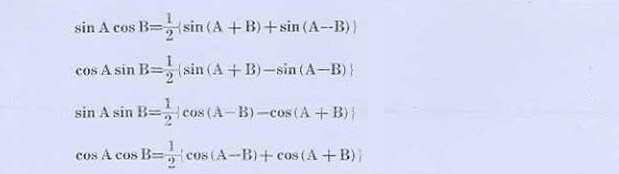
2.평면삼각법

     1)싸인법칙

     2)코싸인법칙

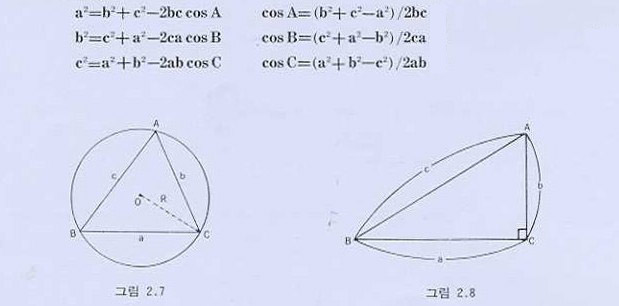
     3)피타고라스의 정리

3.해석기하

    1)직선의 방정식

         ① 기울기(방향계수)가 m, y 축 절편이 b인 직선의 방정식

                y = mx + b

           ② 원점을 통과하는 직선의 방정식

               y = mx

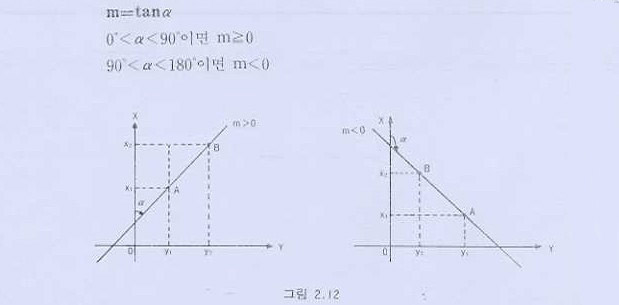
           ③ 직선이 x축과 프러스 방향으로 이루는 각을 α라고 할 때의 기울기 m은

     2)여러 가지 직선의 방정식

         ① 기울기(방향계수)가 m 이고 점(x1, y1)을 지나는 직선의 방정식

                               y - y1 = m (x - x1)

           ② 2점 (x1, y1), (x2, y2)을 지나는 직선의 방정식

           ③ x축, y축 절편이 각각 a, b 인 직선의 방정식

           ④ 원점으로부터 수직거리가  P, 그 수직선이 x축의 프러스 방향으로 이루는 각이 φ 인 직선의 방정식

            ⑤ x 축에 평행하고 y 축 절편이 b인 직선의 방정식

                                y = b

            ⑥ y 축에 평행하고 x 축 절편이 a 인 직선의 방정식

                                 x = a

            ⑦ A, B, C를 정수로 하는 직선의 방정식

                                 Ax + By + C = 0

                                일 때 기울기 m 및 y축 절편 b는

                                       m = -A / B, b = - C / B (B ≠ 0)

 
    3)점과 직선의 거리

            ① 점(x1, y1)으로부터 직선 Ax + By + C = 0 에 내린 수선의 거리

            ② 원점으로부터 직선 Ax + By + C = 0 에 내린 수선의 거리

     4)2 직선의 평행 및 수직조건